テクニカル分析の勉強を始めた頃によくあるシリーズとして
ボリンジャーバンドを使えそうだと思い、使ってしまい失敗する。ということがあります。
ボリンジャーバンドの±2σで収まる確率が95.4%という数字だけを見ると
使えそうだと思ってしまいます。私もその数字でやられた一人です。
※なお、考案したJohn Bollinger(ジョン・ボリンジャー)は
このテクニカルを用いて成功していないので、実質使えないと判断しています。
しかしそういった失敗を避けるために
ボリンジャーバンドの正しい知識と使い方を知ることが大事です。
計算する移動平均線の種類別に学ぶこともですが、
標準偏差の代わりにフィボナッチ級数を使うものも学ぶ必要があります。
今回は計算式と使い方、移動平均線別ボリンジャーバンド12種類、
ボリンジャーバンドフィボナッチの計算式と使い方も解説するため
長くなりますのでご了承ください。
※初心者が手を出すことを避けさせたいのが本記事の狙いです。
ボリンジャーバンドを使うより、1つ1つの波とその組み合わせであるトレンドを
見分ける練習をすることがベストです。
- ボリンジャーバンドとボリンジャーバンドフィボナッチの計算式
- ボリンジャーバンド の形状
- 移動平均線種類別のボリンジャーバンド/ボリンジャーバンドフィボナッチ比較
- 単純移動平均線(SMA:Simple Moving Average)
- 指数関数移動平均線(EMA:Exponential Moving Average)
- 加重移動平均線(WMA:Weighted Moving Average)
- 二重指数関数移動平均線(DEMA:Double Exponential Moving Average)
- 三重指数移動平均(TEMA:Triple Exponential Moving Average)
- 三角移動平均線(TRIMA:Triangular Moving Average)
- カウフマン適応移動平均線(KAMA:Kaufman’s Adaptative Moving Average)
- MESA適応型移動平均線(MAMA:MESA Adaptive Moving Average)
- T3移動平均線(T3:T3 Moving Average)
- ハル移動平均線(HMA:Hull Moving Average))
- 線形加重移動平均(LWMA:Linear Weighted Moving Average)
- 平滑移動平均線(SMMA:Smoothed Moving Average)
- まとめ
- エリオット波動を実践用にまとめた手法レポートを持っておくと便利!
- 裁量トレードをシンプルに!エントリー、リスクリワードを高められる取引方法
ボリンジャーバンドとボリンジャーバンドフィボナッチの計算式
ボリンジャーバンドは、以下のことから定義されて作られたものです。
⑴移動平均線・・・ある期間の平均価格を知るため
(計算式や四本値のどれを採用するかによって変わる)
⑵標準偏差・・・平均からどのくらい離れているかを知るため
⑶ストキャスティクス・・・ある期間内のボラティリティを知るため
ストキャスティクスの概念を飛ばしている人が多いですが、
ボリンジャーバンドの売られ過ぎ、買われ過ぎという誤解は
ストキャスティクスの部分からきています。
ストキャスティクスの計算式から、チャートで読み取る4つのこと
偏差という言葉から偏差値という言葉が浮かびやすいですが、
偏差値が高いからといって急に落ちる訳でもなく、さらに上がっていくことも
十分あり得る訳で、偏差の結果から〜すぎるという言葉は絶対に生まれないはずなのです。
ボリンジャーバンドフィボナッチはATRという「真の値幅の平均」 にフィボナッチ級数を掛けたものですが
これに関しても〜すぎるという言葉は生まれません。
そういったことを理解した上で、計算式をそれぞれ見ていきましょう。
ボリンジャーバンドの計算式
ミドルライン:n期間の移動平均
±1σ: n期間の移動平均 ± n期間の標準偏差
±2σ: n期間の移動平均 ± n期間の標準偏差 × 2
±3σ: n期間の移動平均 ± n期間の標準偏差 × 3
標準偏差=√(n×n期間の終値の2乗の合計-n期間の終値の合計の2乗)÷(n×(n-1))
±1σの範囲内に収まる確率・・・約68.3%
±2σの範囲内に収まる確率・・・約95.4%
±3σの範囲内に収まる確率・・・約99.7%
ボリンジャーバンドフィボナッチの計算式
ミドルライン:n期間の移動平均
±1ライン: n期間の移動平均 ±n期間ATR×1.618
±2ライン: n期間の移動平均 ±n期間ATR×2.618
±3ライン: n期間の移動平均 ±n期間ATR×4.618
⑴当日の高値と前日の終値の差→当日の高値-前日の終値
⑵前日の終値と当日の安値の差→前日終値-当日安値
⑶当日の高値と当日の安値の差→当日の高値-当日の安値
以上のうちもっとも大きいものがTR
ATR=TRのn期間の指数平滑移動平均値
ATRについては後日改めて解説します。
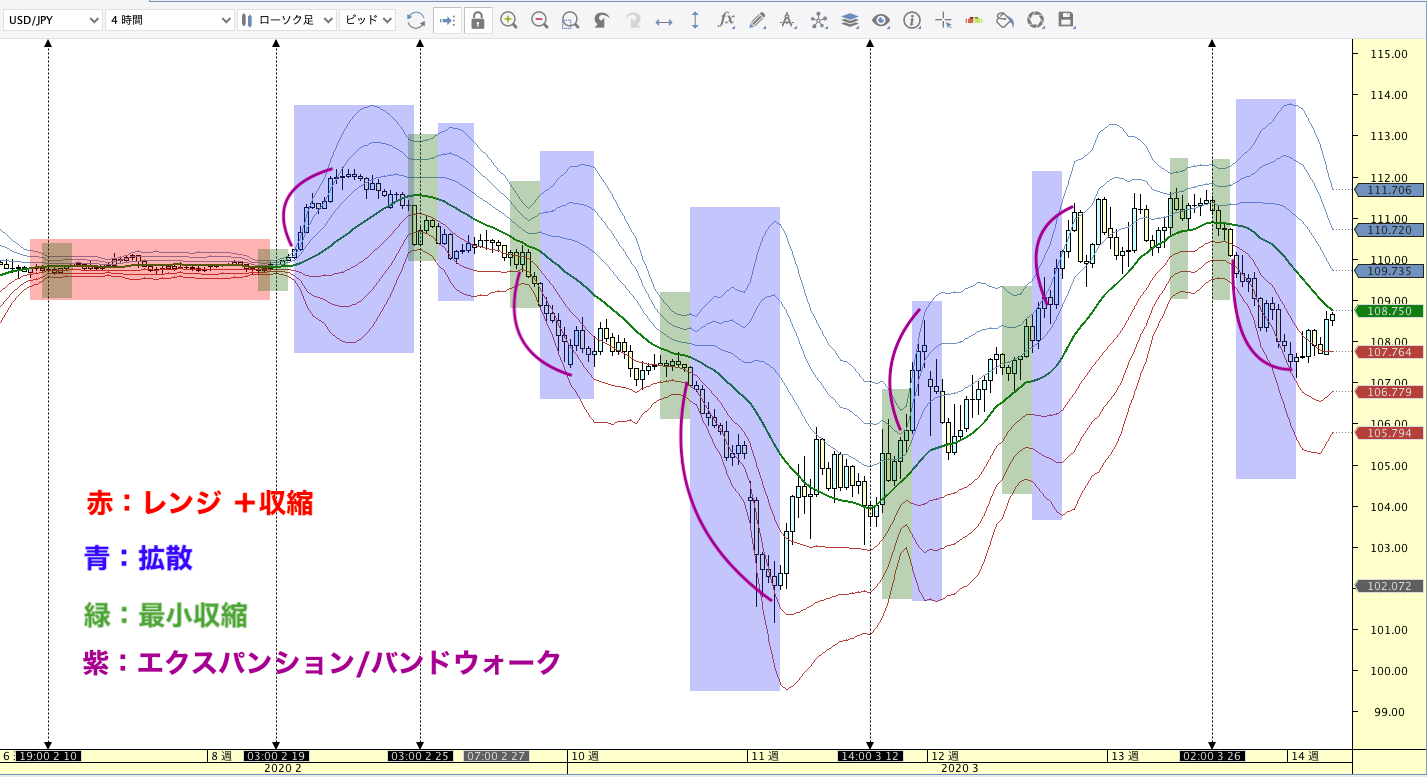
ボリンジャーバンド の形状
用語は紹介されているサイトによって違いますので、覚える必要はありません。
収縮しているか、拡散しているか、±2σ上で動いているバンドウォーク/エクスパンションかを
把握できていれば十分です。
このようにすでに出来上がったチャートで解説するのは簡単ですが、
ボリンジャーバンドをリアルタイムで把握していくのは初心者は難しいです。
これが勘違いを生む原因の1つです。
ボリンジャーバンドのトレード例を過去チャートで上げているサイトが多いですが
実際にトレードする場面でそのような解釈をしていくのは厳しいです。
初心者が手を出すことを避けさせたいのが本記事の狙いです。
ボリンジャーバンドを使うより、1つ1つの波とその組み合わせであるトレンドを
見分ける練習をすることがベストです。
それができて初めて効果的なトレンドラインや平行線(サポート/レジスタンスライン)などが引けるため
ボリンジャーバンドは全てできるようになってからで遅くはありません。
移動平均線種類別のボリンジャーバンド/ボリンジャーバンドフィボナッチ比較
というわけで、1つ1つの波とそれらを組み合わせたトレンドを見分けられた方は
この後の移動平均線種類別のボリンジャーバンド 、ボリンジャーバンドフィボナッチを
見比べてください。
それぞれの移動平均線の種類の計算式も載せているので、理解を深めるためにも
参考にしてください。
なお、全てのチャートの基本設定は、期間:20,Price:Close(終値)です。
PriceがOpen、High、Low、Median(HL/2)、Typical(HLC/3)、Weighted Close(HLCC/3)によって
計算値が変わるため、表示が若干変わります。
またボリンジャーバンド は2σのみ、
ボリンジャーバンドフィボナッチは[1.618]、[2.618]、[4.618]のバンドを表示しています。
単純移動平均線(SMA:Simple Moving Average)
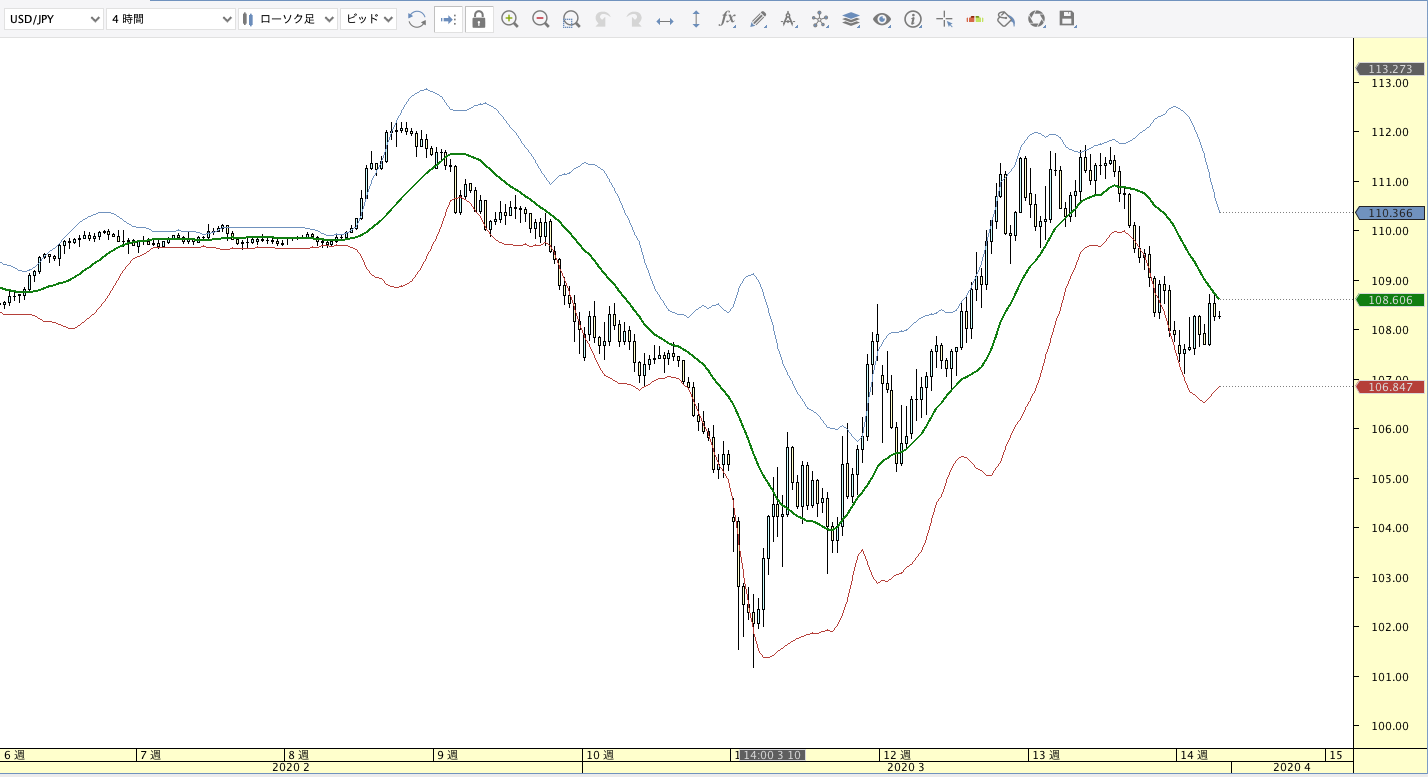 |
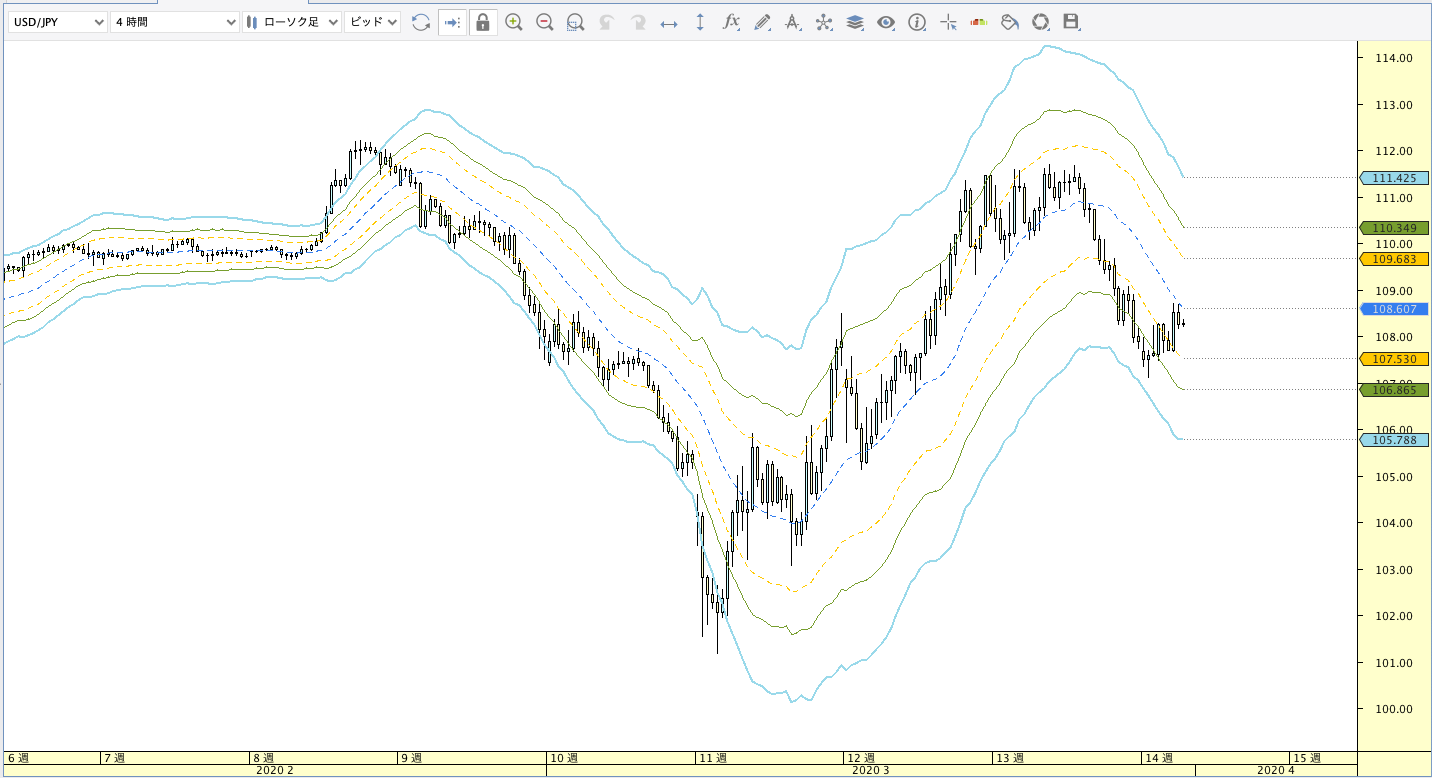 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
SMA計算式
SMA(n)={終値0+終値1+・・・終値(n-1)}÷n
nは任意の期間
指数関数移動平均線(EMA:Exponential Moving Average)
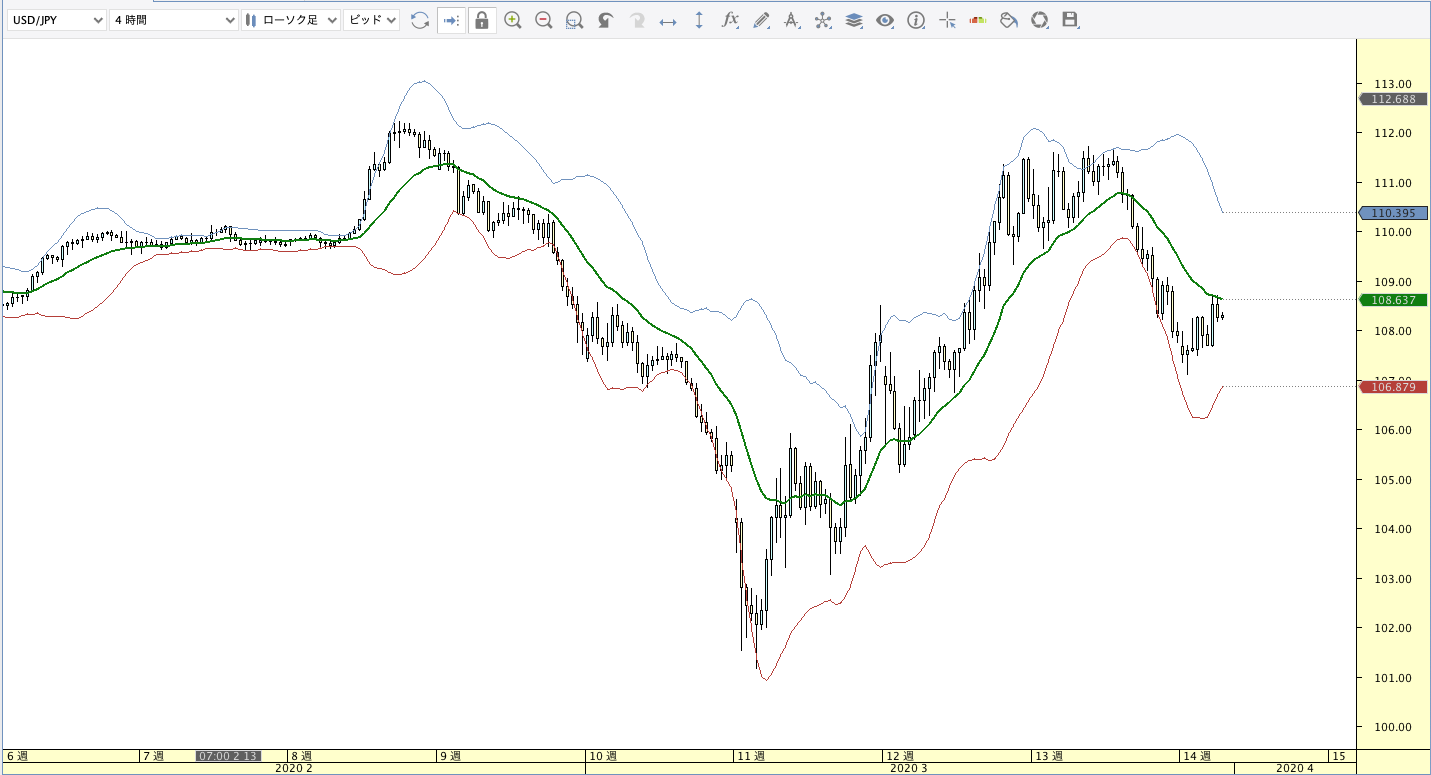 |
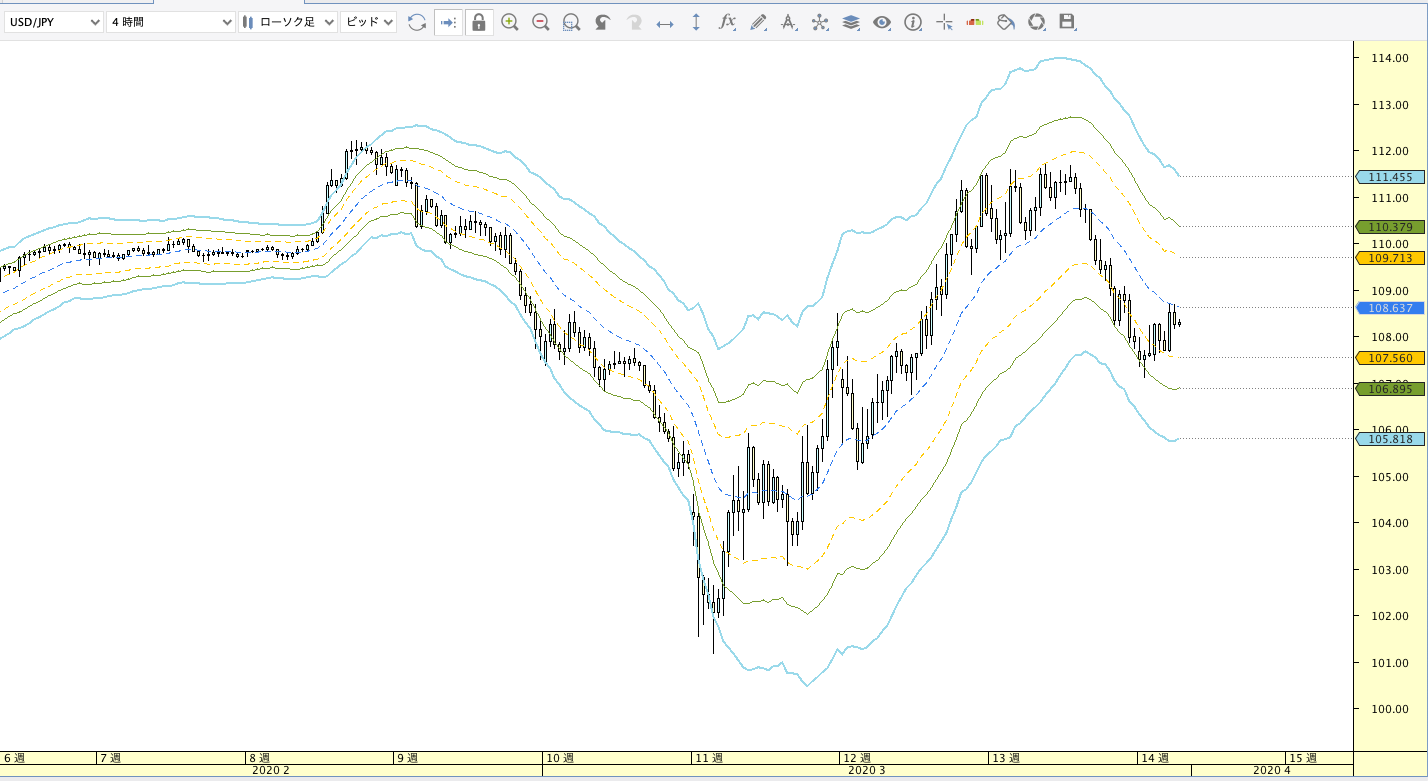 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
EMA計算式
最初の計算式はSMA{終値0+終値1+・・・終値(n-1)}÷n
EMA(n) = 前日EMA+α×(当日終値-前日EMA)
α(平滑化定数) = 2÷(n+1)
nは任意の期間
加重移動平均線(WMA:Weighted Moving Average)
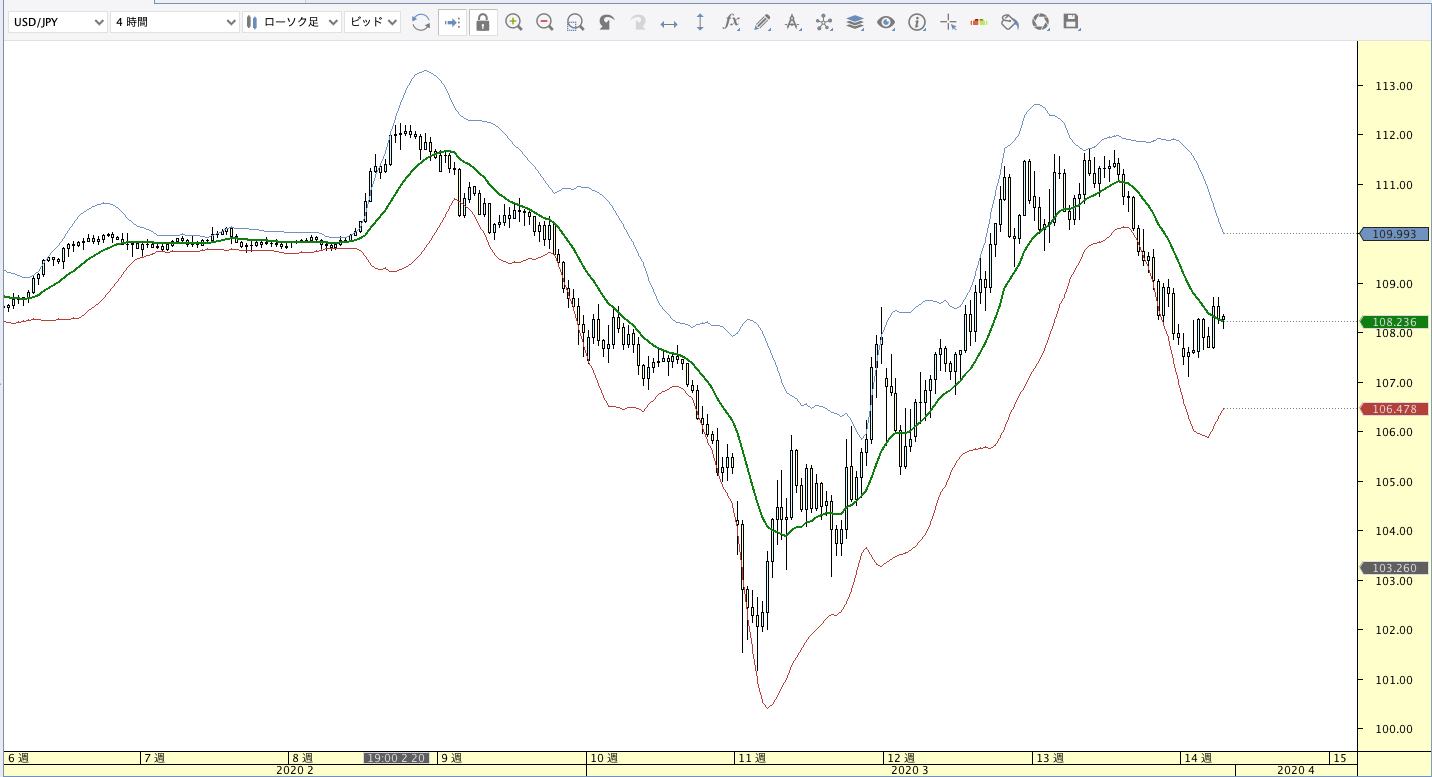 |
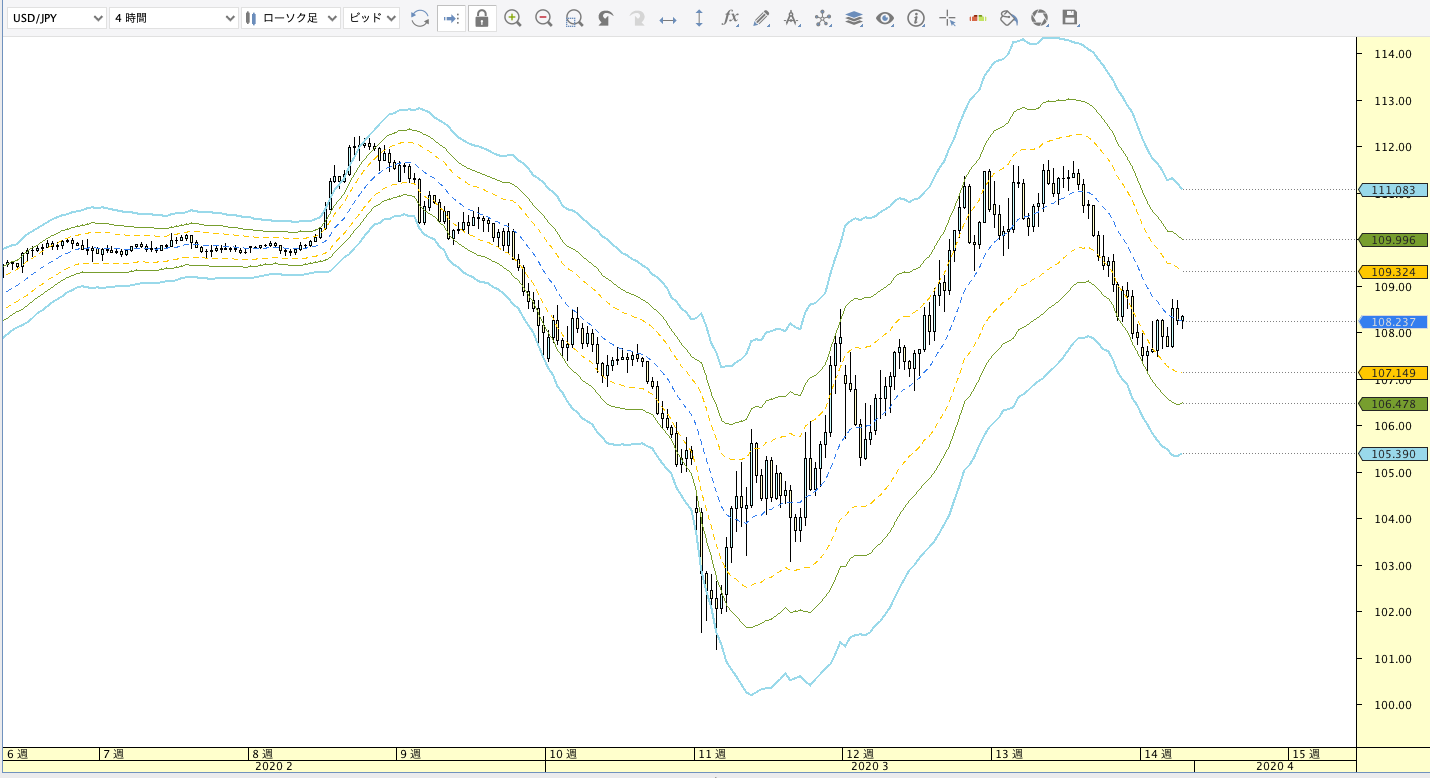 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
WMA計算式
WMA(n) ={ n×終値0+(n-1)×終値1・・・+-1×終値n-1}÷n!(nの階乗)
nは任意の期間
(例)10WMA
(10×当日終値+9×前日終値+8×一昨日終値・・・1×9日前終値)÷
(10+9+8・・・+1)
二重指数関数移動平均線(DEMA:Double Exponential Moving Average)
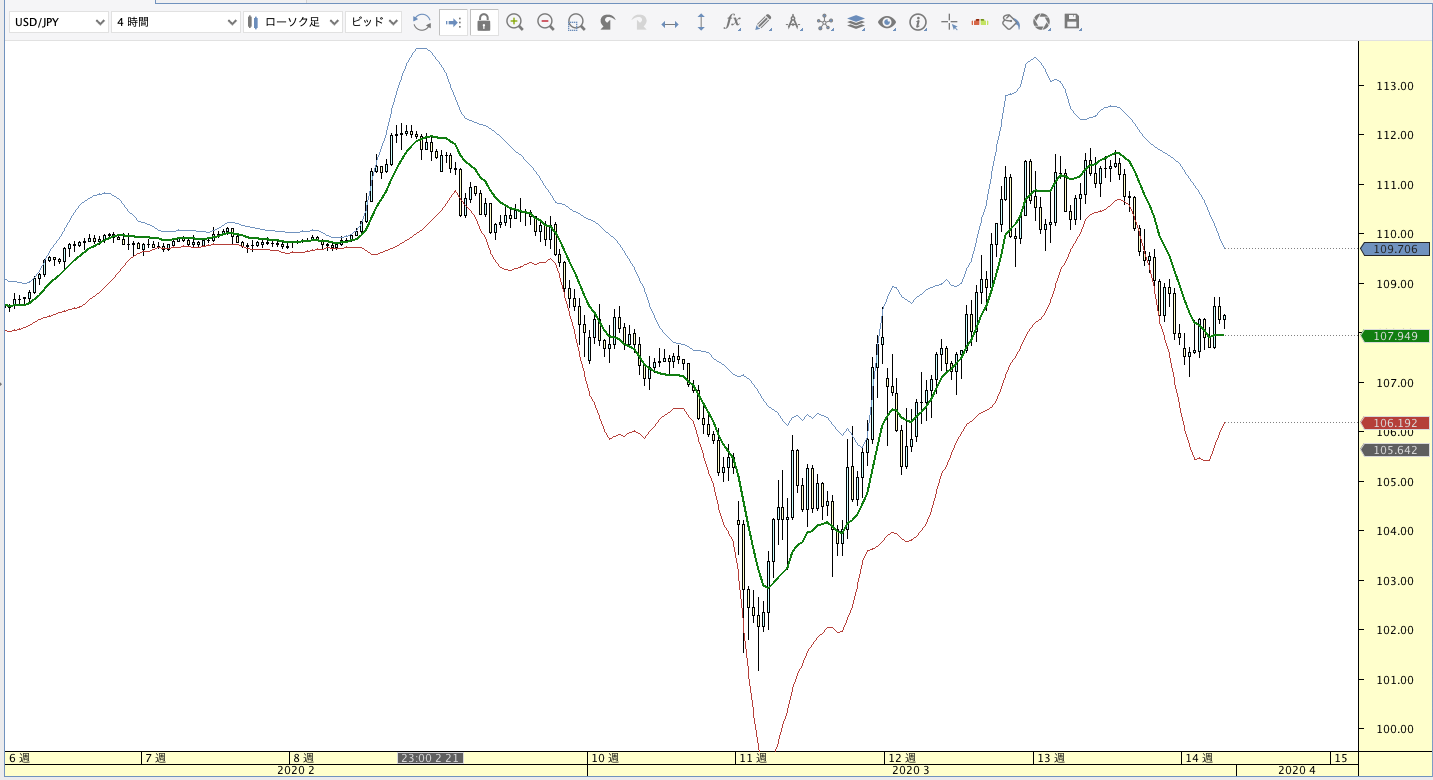 |
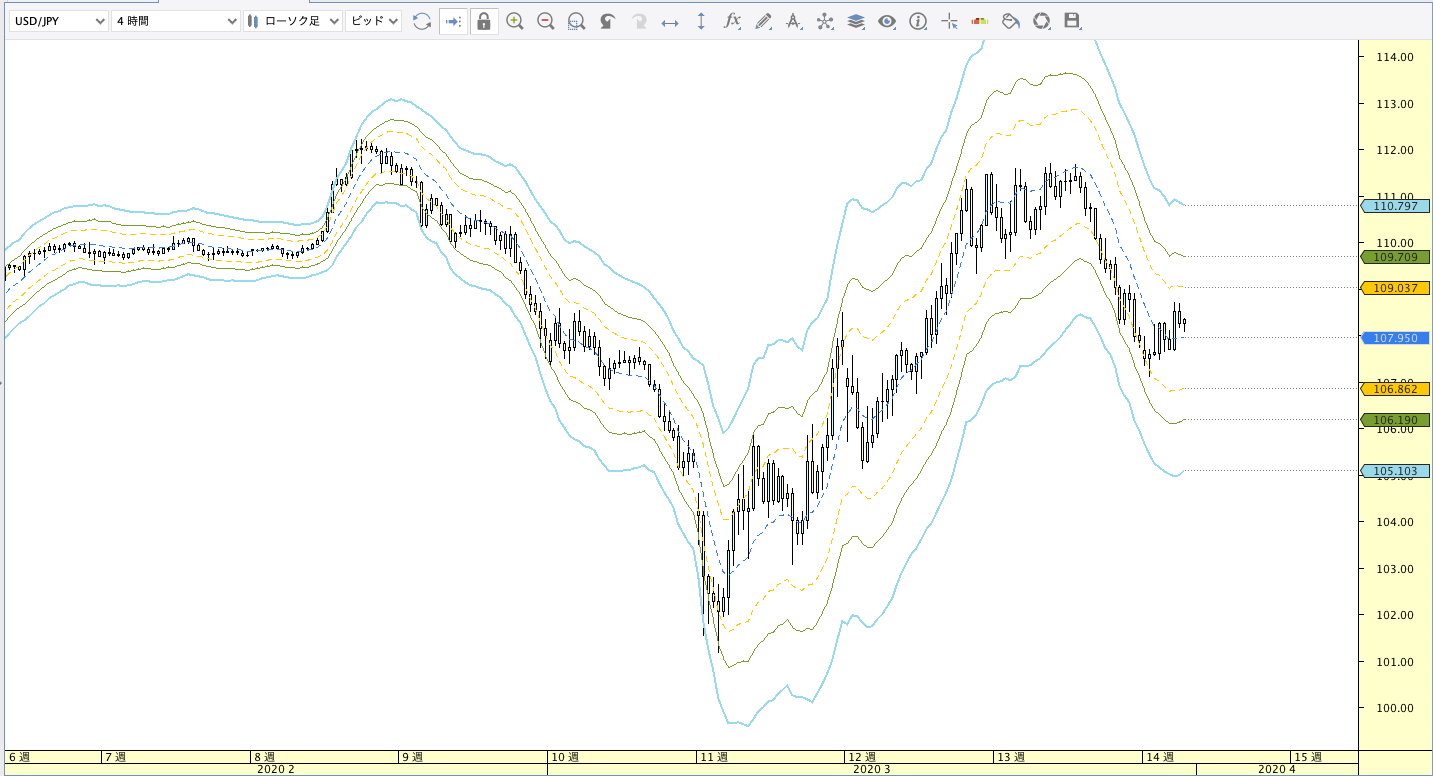 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
DEMA計算式
DEMA(n) = 2EMA (n)- EMA(EMA(n))
nは任意の期間
n期間のEMAを2倍したものから、n期間のEMAを2回掛けたものを引きます。
三重指数移動平均(TEMA:Triple Exponential Moving Average)
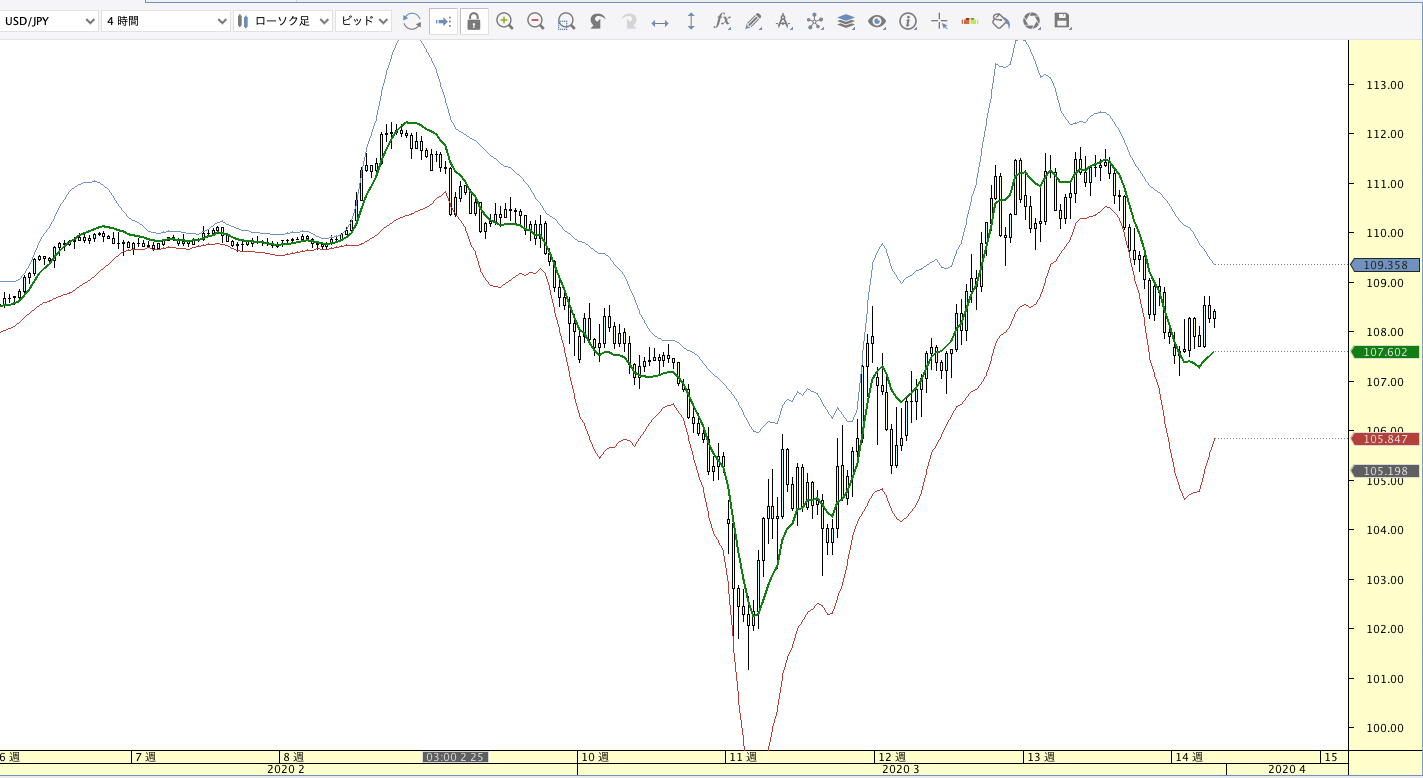 |
 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
TEMAの計算式
TEMA(n) = 3EMA- 3EMA(EMA(n)) + EMA(EMA(EMA(n))
nは任意の期間
三角移動平均線(TRIMA:Triangular Moving Average)
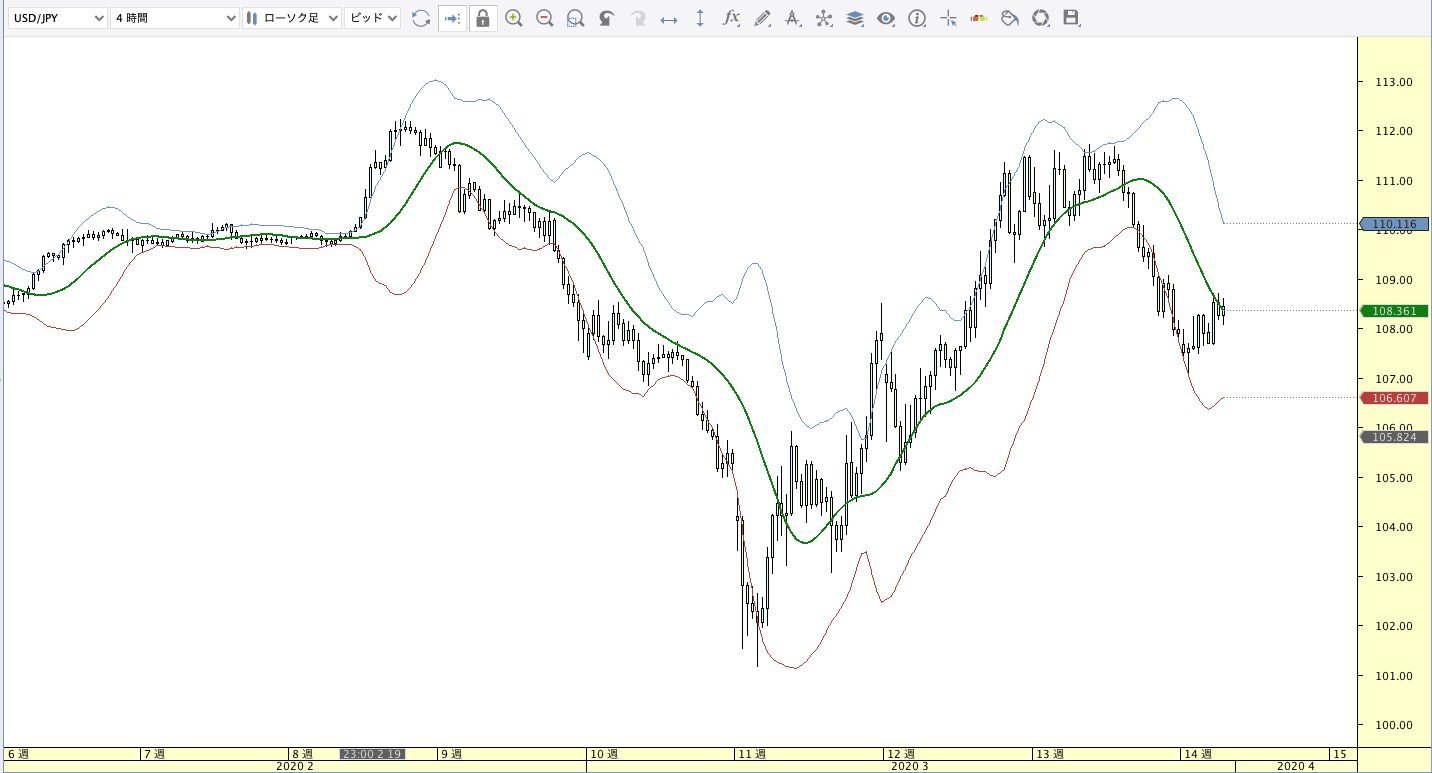 |
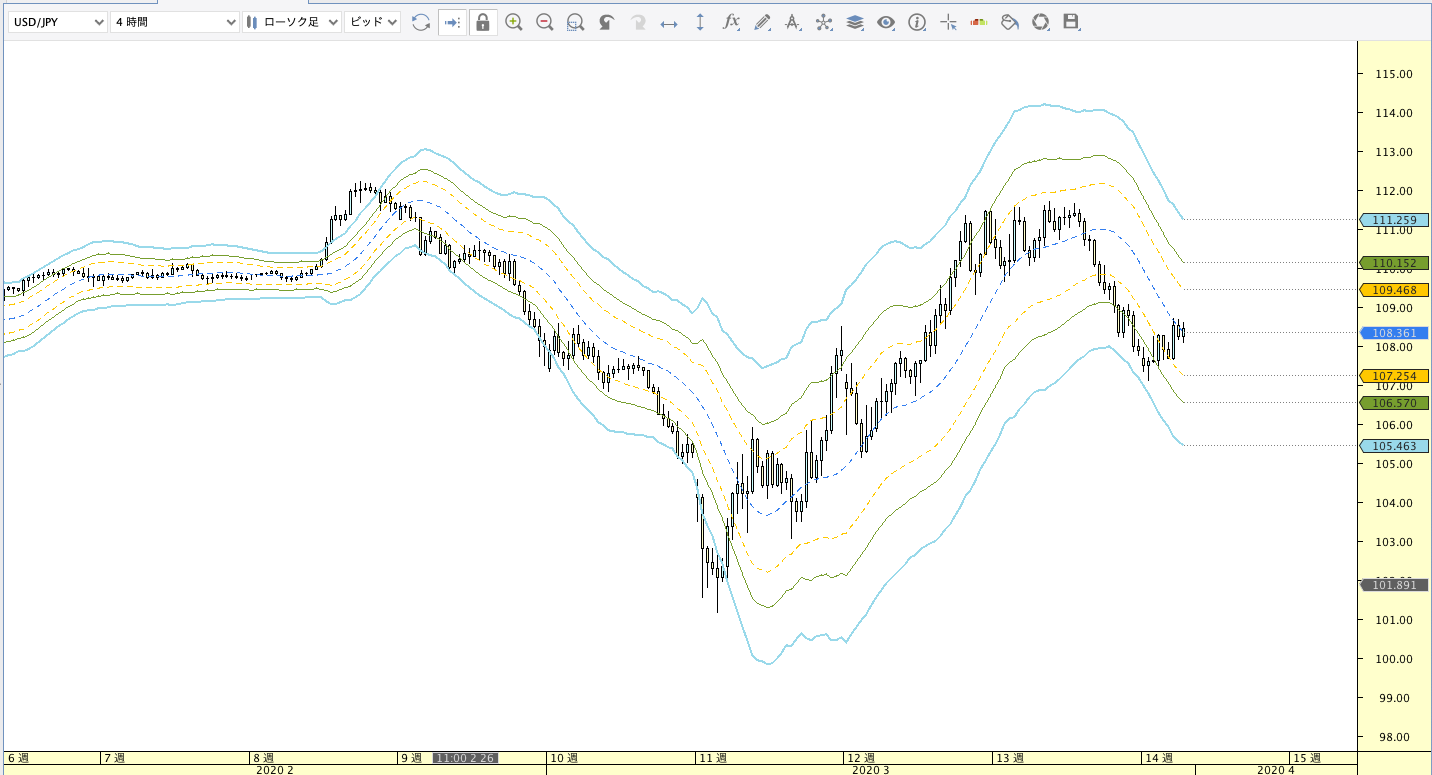 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
TRIMA計算式
TRIMA(n)=SMA(α,SMA(α,終値))
nは任意の期間
移動平均日数(α)=(n+1)÷2
※計算日数が奇数になったら切り上げる
n期間の中間点を重視して加重する、移動平均を移動平均で平滑化したもの。
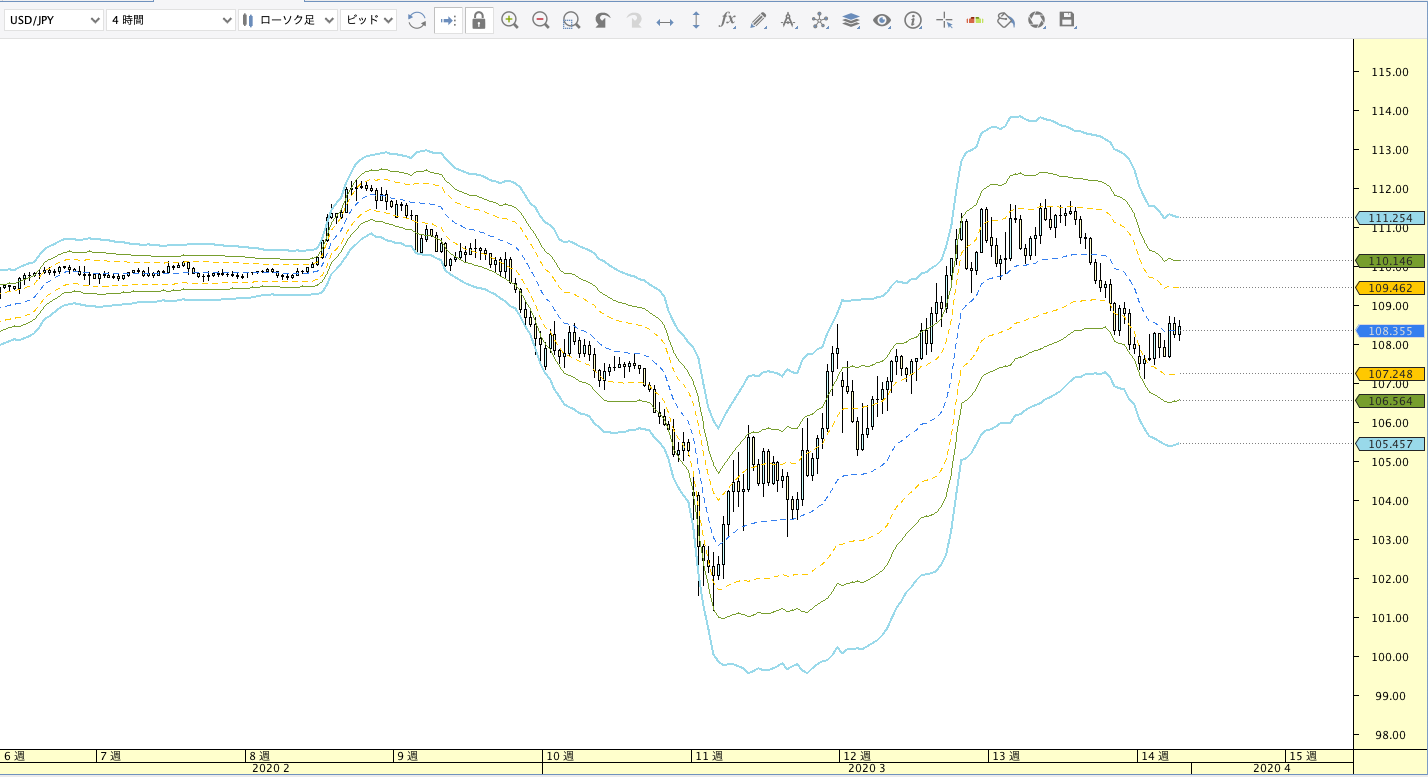
カウフマン適応移動平均線(KAMA:Kaufman’s Adaptative Moving Average)
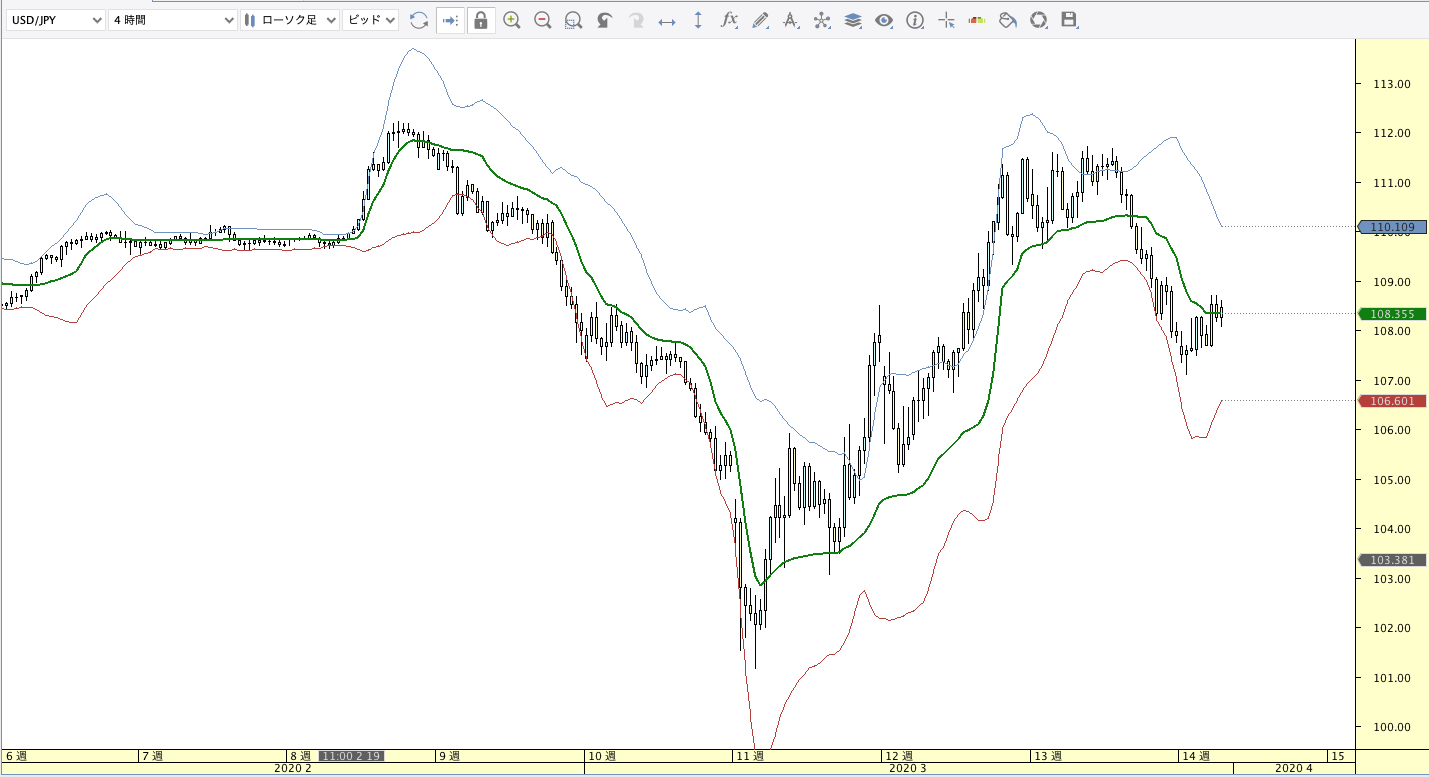 |
 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
KAMA計算式
KAMA(n)=前日KAMA + (当日終値 - 前日KAMA) × SC
SC=[2/{(x+y)-2/(y+1)}×ER+2/(y+1)]2
ER={(終値 - n日前の終値)/n日間の前日比の絶対値の合計}2
n,x,yは任意
ペリーカウフマン(Perry.J.Kaufman)が考案した移動平均線を
その時点でのトレンドの勢いに適応させるために算出方法を変え、
有効な回帰値を求めたもの。
「平滑化定数」の変化は効率レシオ(Efficiency Ratio(ER))の絶対値と
2つの定数を使って求める。
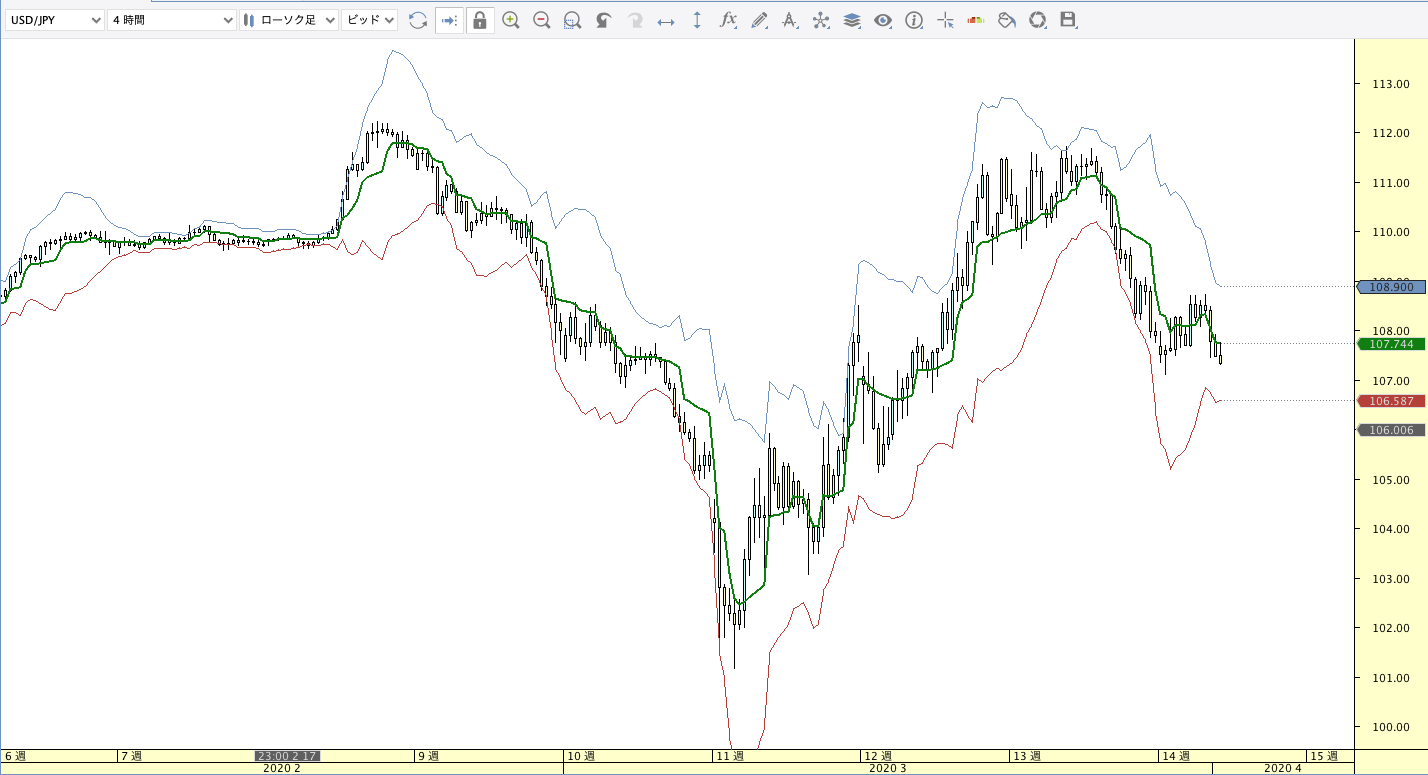
MESA適応型移動平均線(MAMA:MESA Adaptive Moving Average)
 |
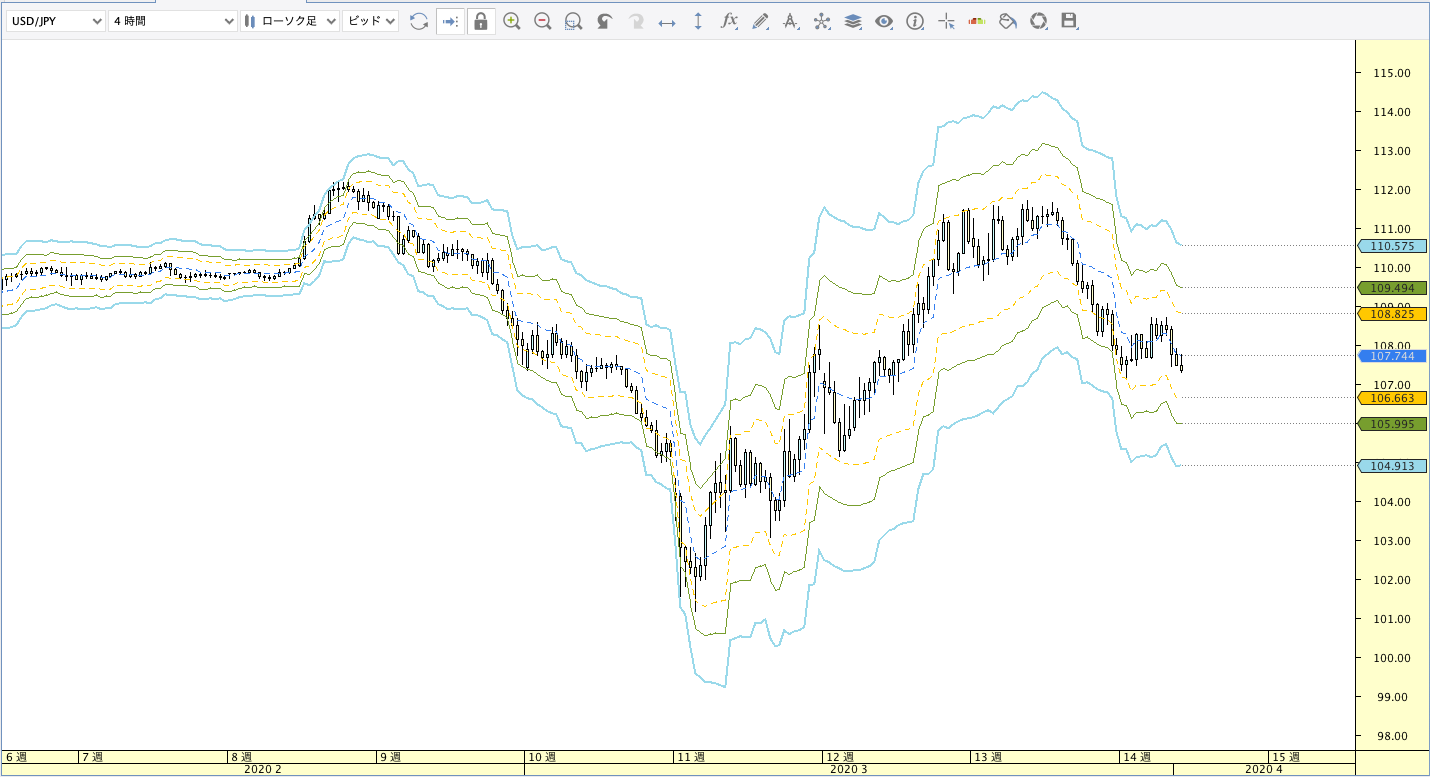 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
MAMA計算式がわかり次第追記
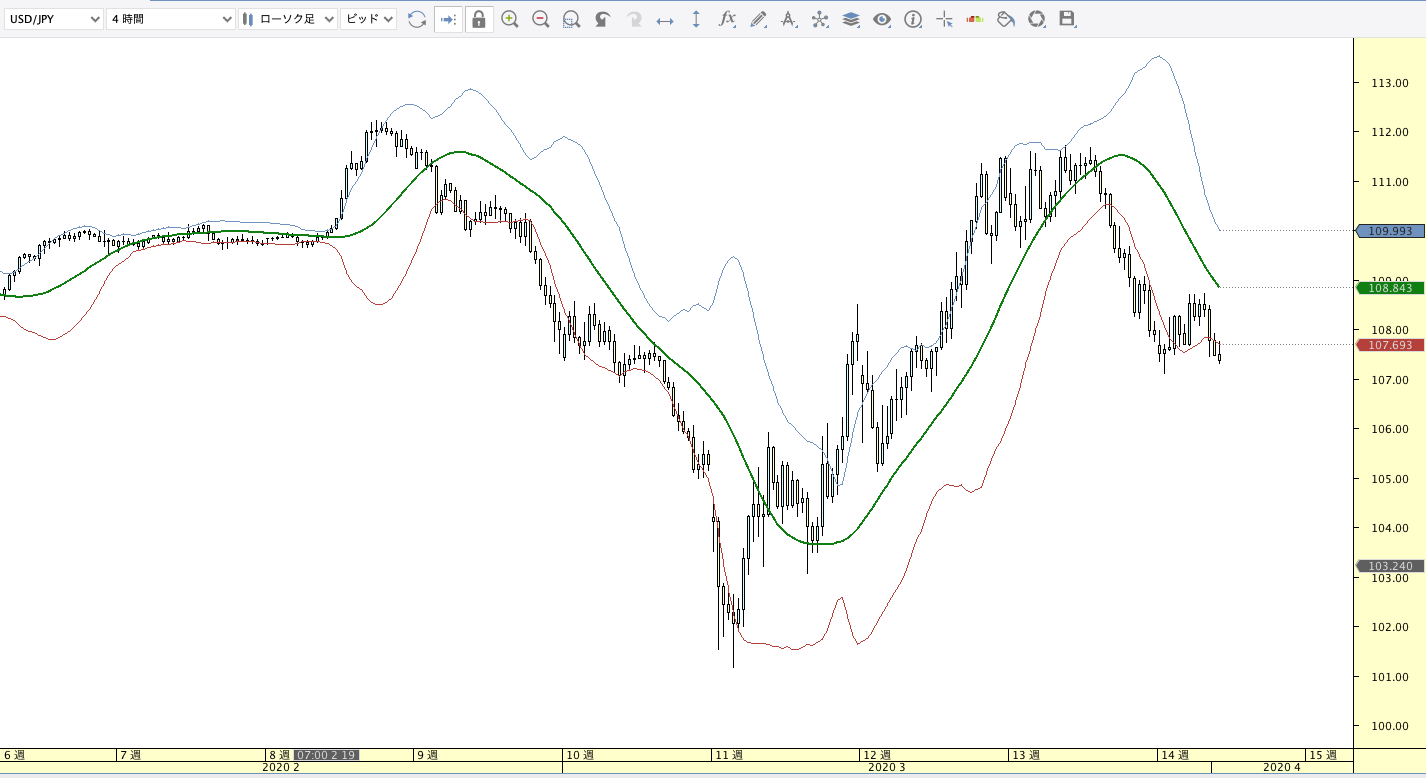
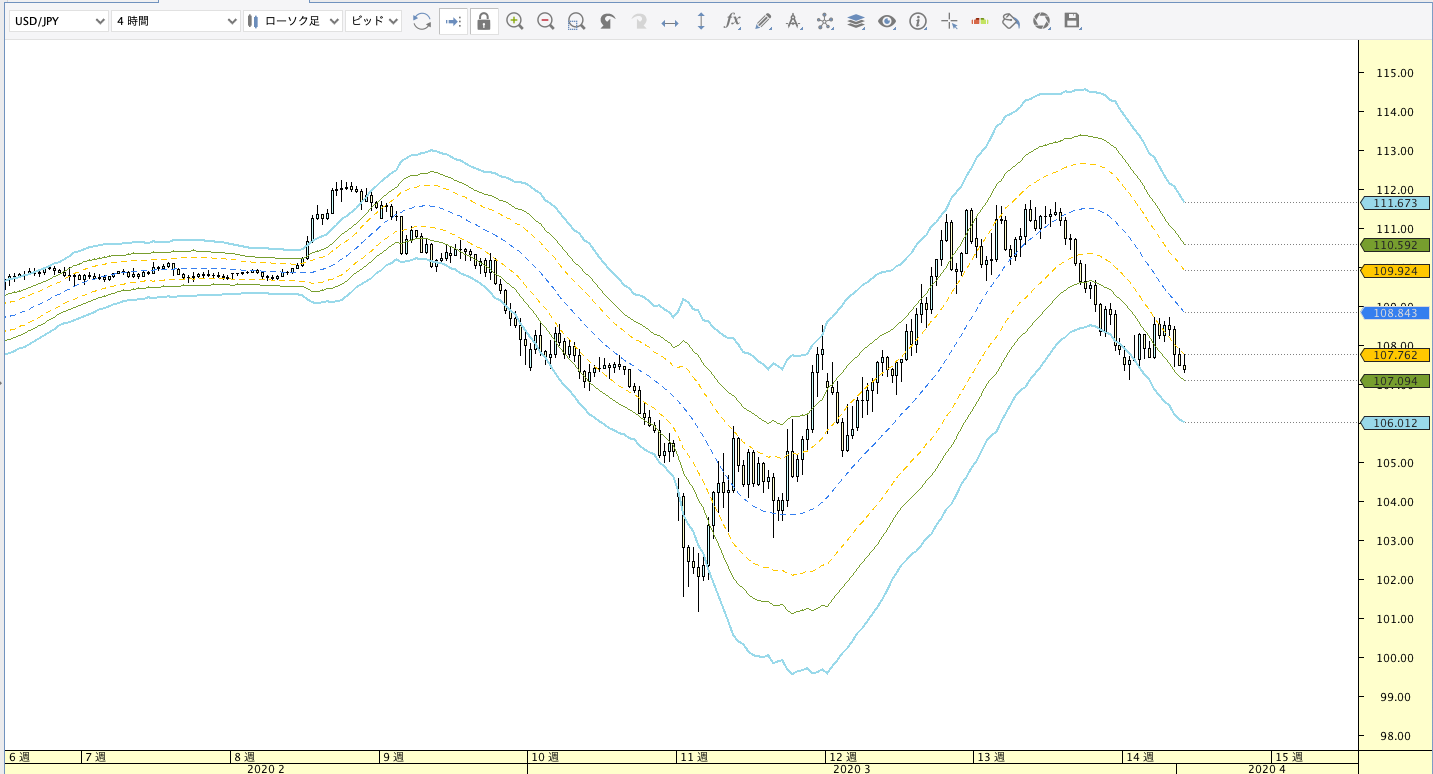
T3移動平均線(T3:T3 Moving Average)
 |
 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
T3計算式
T3(n)=EMA(n) × (1 + f) – EMA2(n) × f
EMA(n)はn期間指数移動平均
EMA2(n)はn期間指数移動平均のn期間指数移動平均
fは0~1の間の数字。通常はf=0.7
nは任意
Tim Tillson(ティム・ティルソン)によって開発された移動平均線で、
3重のDEMAのことです。
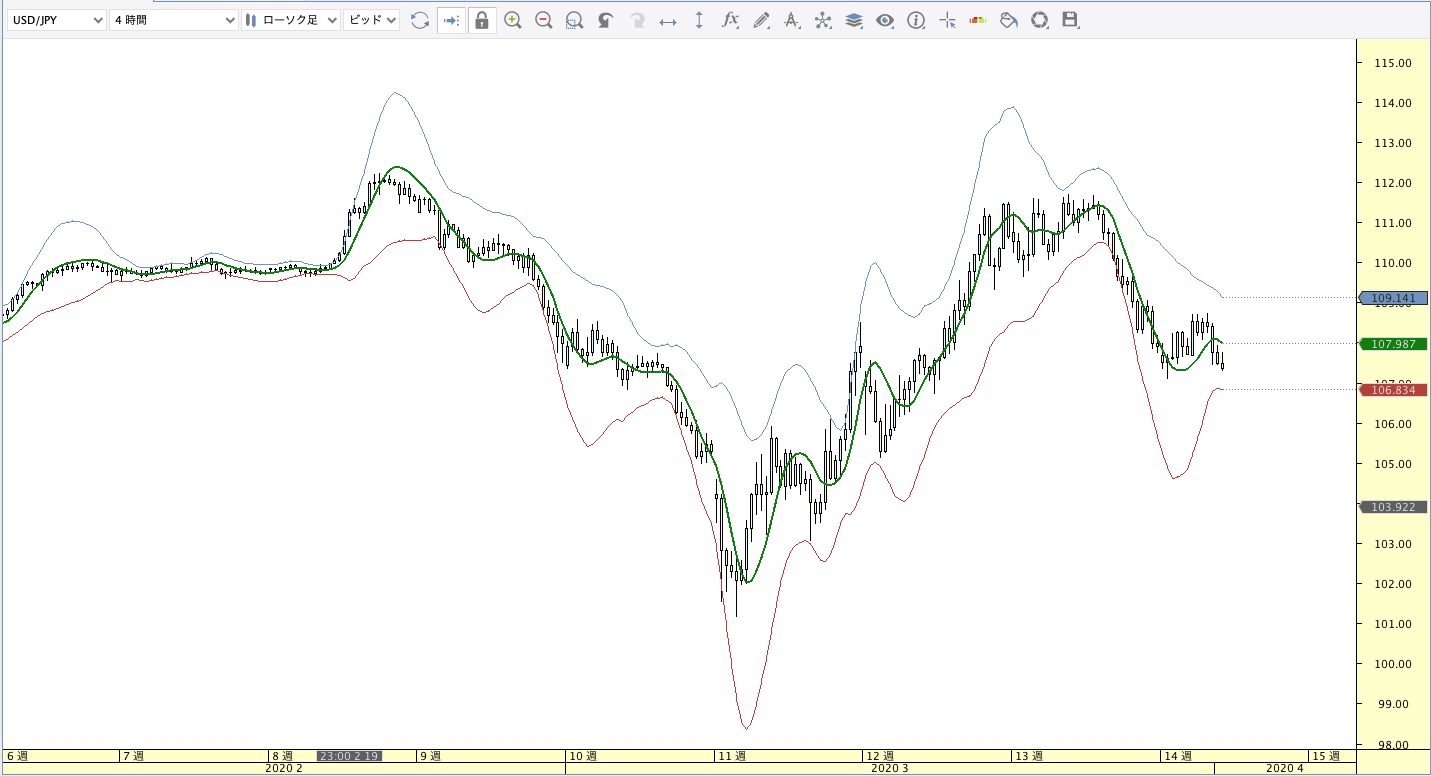
ハル移動平均線(HMA:Hull Moving Average))
 |
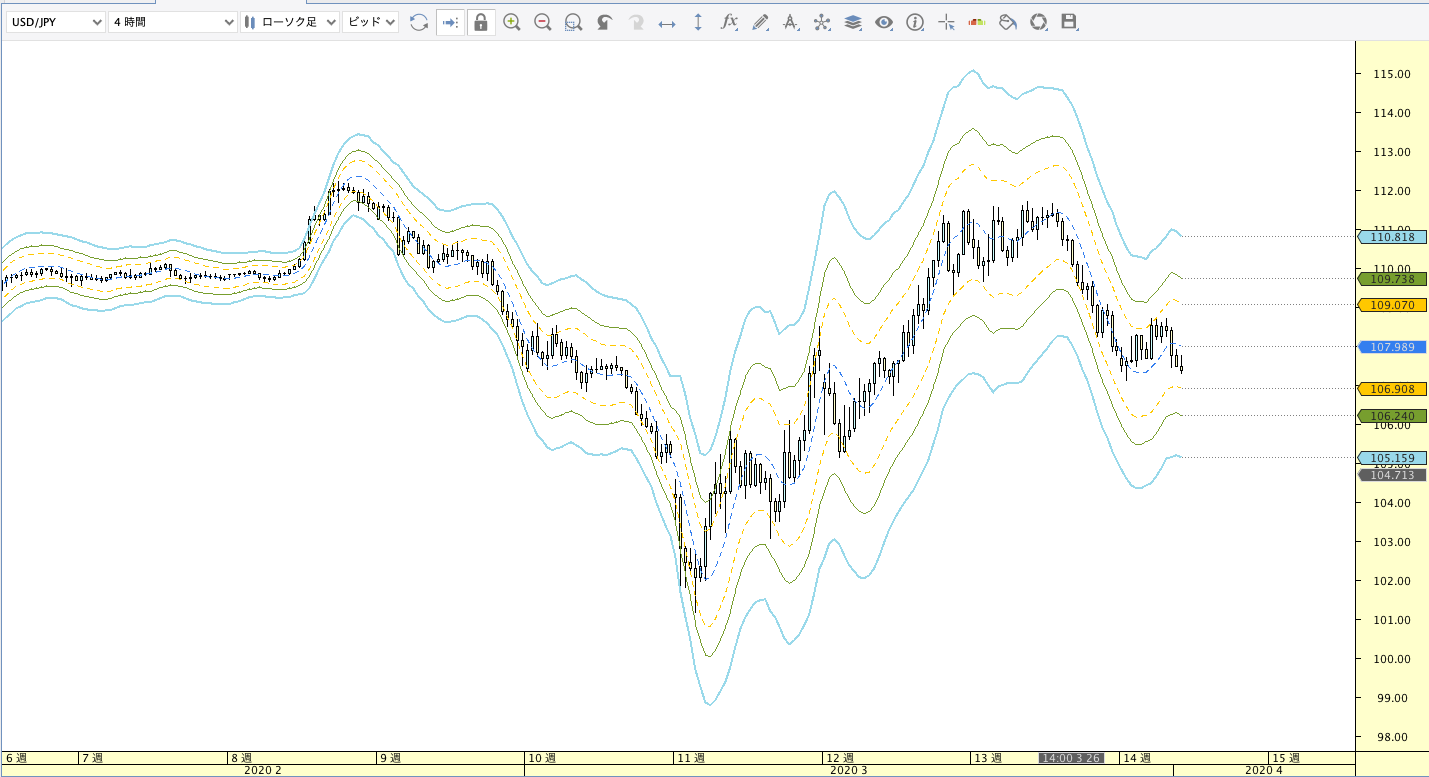 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
HMA計算式
HMA(n) = WMA(n/2) × 2 – WMA(n)
nは任意の期間
線形加重移動平均(LWMA:Linear Weighted Moving Average)
 |
 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
LWMA計算式(WMAと同じ)
LWMA(n)={ n×終値0+(n-1)×終値1・・・+-1×終値n-1}÷n!(nの階乗)
nは任意の期間
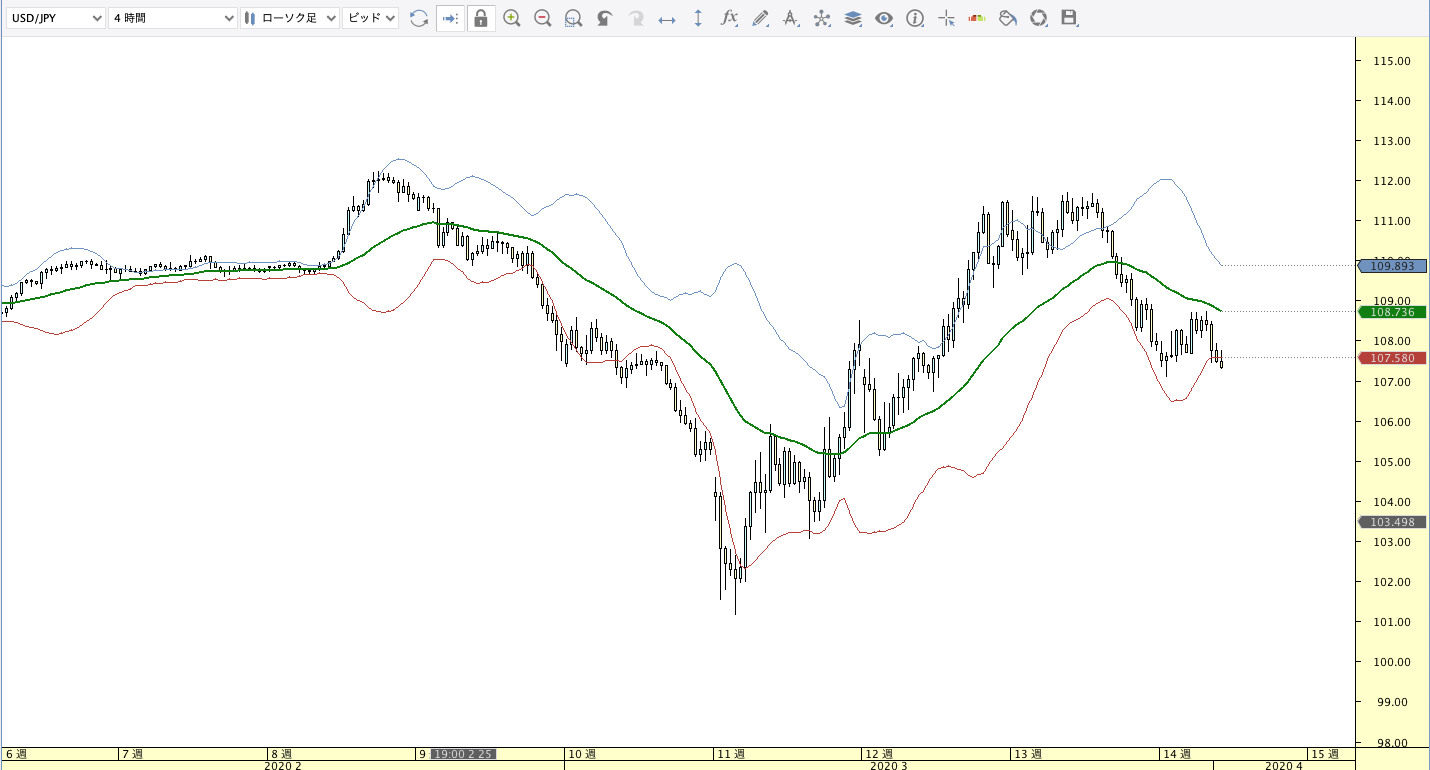
平滑移動平均線(SMMA:Smoothed Moving Average)
 |
 |
| ボリンジャーバンド | ボリンジャーバンドフィボナッチ |
SMMA計算式
SMMA(n)={(n-1)×前日SMMA+当日終値}÷n
nは任意の期間
Running Moving Average(RMA)、Modified Moving Average(MMA)とも呼ばれる。
まとめ
ボリンジャーバンドとボリンジャーバンドフィボナッチの違いは
ボリンジャーバンドが移動平均線と標準偏差を元にし、
ボリンジャーバンドフィボナッチは移動平均線とATRにフィボナッチ級数を掛けたものでした。
(フィボナッチ級数基本設定:1.618、2.618、4.618)
ボリンジャーバンド2σに収まる確率は95.4%、3σで99.7%ですが
これはあくまでその位置にあるということなので、バンドウォークのような
トレンドが出た相場では2σ〜3σの間で推移することが多くなります。
バンド幅が両方広がっているか片方しか広がらない、
または両方とも狭まるか片方しか狭くならない状態によって考え方が変わります。
両方とも広がっていればトレンドが出ており、狭まっていればトレンドがない状態です。
片方しか広がらない、または狭まらない場合は、逆方向へいくか、次の動きを模索している段階です。
これをリアルタイムで把握することが肝になります。
大抵はどちらかを見落としていたりするため、他のインディケーターを使った手法より
疲れてしまったり、ラインが多くなるため間違えることが多くなります。
もし使う場合はしっかりとリアルタイムで見ていきながら練習してください。





コメント